1.引言
近年来,随着移动互联网和下一代无线通信系统的发展和演进,用户对于高速率传输有了广泛的需求。为了迎合这种需求,越来越多的移动终端采用了多天线技术,即多输入多输出(Multiple- Input-Multiple-Output, MIMO)技术。
然而,由于工业设计和产品外观的要求,多天线之间的间距远小于半波长,在如此紧凑的空间中摆放多个天线,会造成天线之间的强互耦和强相关。强互耦会降低天线自身的辐射效率。低效率强相关的多天线系统传输的数据速率会明显降低[1]。
为了解决这种互耦问题,简称为解耦或去耦问题,目前学术界和工业界已经提出了多种方法。包括传输线解耦[2],正交模式解耦[3],以及利用一些特殊的辐射或谐振结构解耦[4,5]。然而,目前缺乏一种简单的,易集成的以及与不依赖天线本身特性和形式的解耦方法。
2.天线去耦合芯片介绍
朗普达提出了一种崭新的解耦概念,利用两个或多个耦合的谐振器网络,并联或级联在两天线或多天线上,通过合理的综合设计网络参数,达到解耦和天线匹配的效果[6]~[8],这种去耦合芯片,被称为“天线去耦合芯片”,简称AIR(AntennaInterference Reduction),其基本电路原理图,请见图1。其主要特性有:
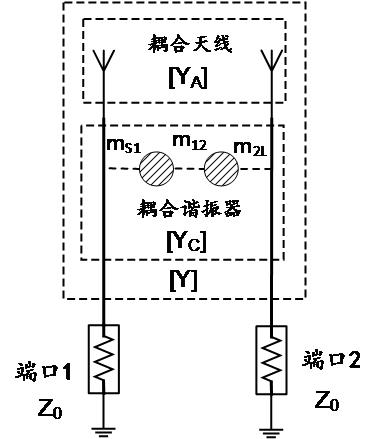
图 1 天线去耦合芯片电路原理图
1) 体积小,易于集成。最新的基于低温共烧陶瓷技术的尺寸可以小到,非常适合移动终端使用。
2) 此网络有一套可以根据天线参数进行综合设计的理论。由于网络参数可控,AIR往往能实现相对较宽的解耦带宽。
3) AIR不依赖天线形式和参数,只要确定了谐振频率,AIR有一套机理可以调节以适应各种天线。
4)AIR本身的参数特性,保证了在解耦的时候,不破坏天线本身的匹配
3.天线去耦合芯片基本原理
如图1所示,一对耦合天线可以用一个二乘二的矩阵[YA]来表示,一般的,这个矩阵中的元素都是复数。而若干耦合在一起的,无耗的微波谐振器,则也可以用一个纯虚数的矩阵[YC]来表示。两个网络并联所得到的总网络[Y],可以表示为:
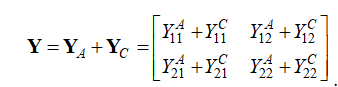
由公式(1)可以得到总网络的解耦条件和匹配条件如下:
解耦条件:
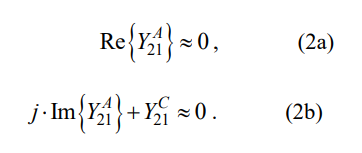
匹配条件:
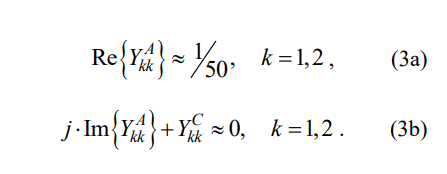
条件(2a)和(3a)对于谐振在感兴趣的频点处的一对耦合天线,总是近似满足的。设计者还可以设计一段传输线,使(2a)更好的满足[8]。而剩余的条件(2b)和(3b)则需要根据天线特性,合理的综合设计天线去耦合芯片的各耦合系数:mS1, m12及m2L.具体的综合理论已在[8]中详述。当然,设计者也可利用电路仿真软件Advanced Design System进行优化设计,使得AIR的耦合系数满足条件(2b)和(3b).
4.AIR的LTCC实现
为了满足移动终端器件小型化的需求,我们采用了基于0805封装(尺寸)的低温共烧陶瓷(LTCC)技术来实现AIR。采用的材料介电常数为9.8,总共有19层叠层而成。其示意图请见图2。
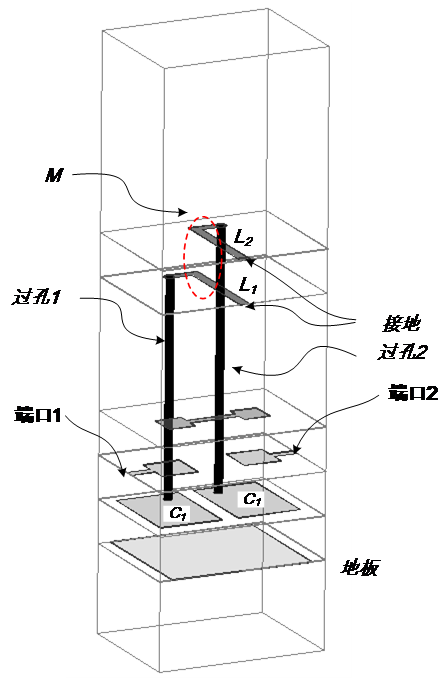
图 2 LTCC实现的两阶AIR模型图
5.AIR的实际应用
我们选取Wi-Fi 2.4GHz频段作为实例,展示AIR在实际天线解耦中的作用。图3的(a)和(b)分别为原始耦合较强的天线以及加入AIR之后的天线。天线均采用柔性印制电路板(FPC)形式制成,天线支架采用了3D打印机设计加工。
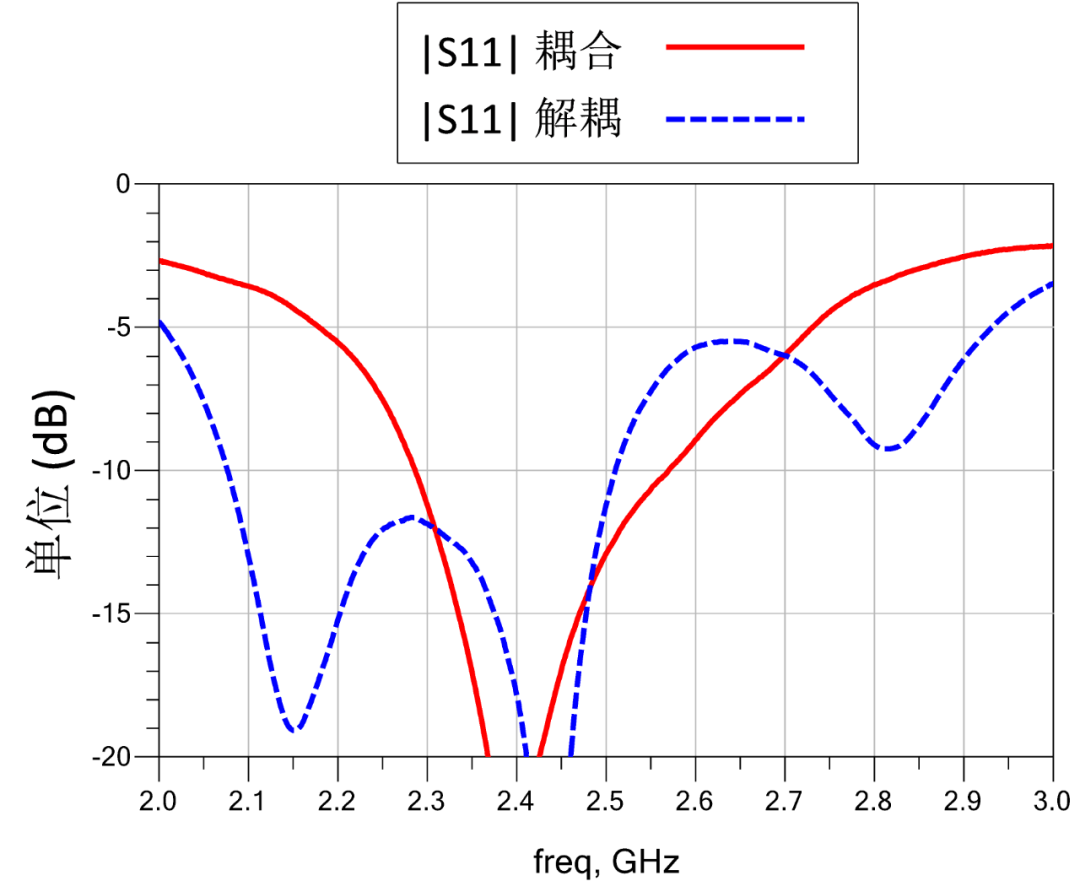
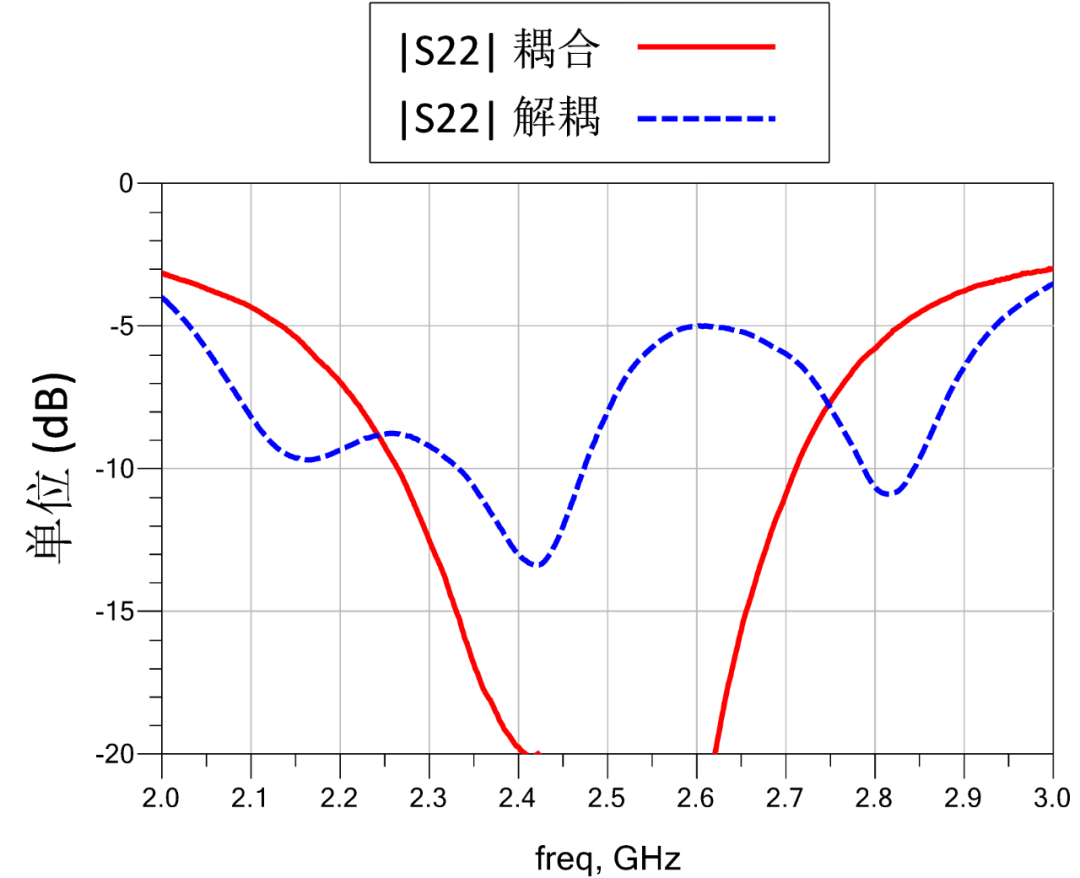
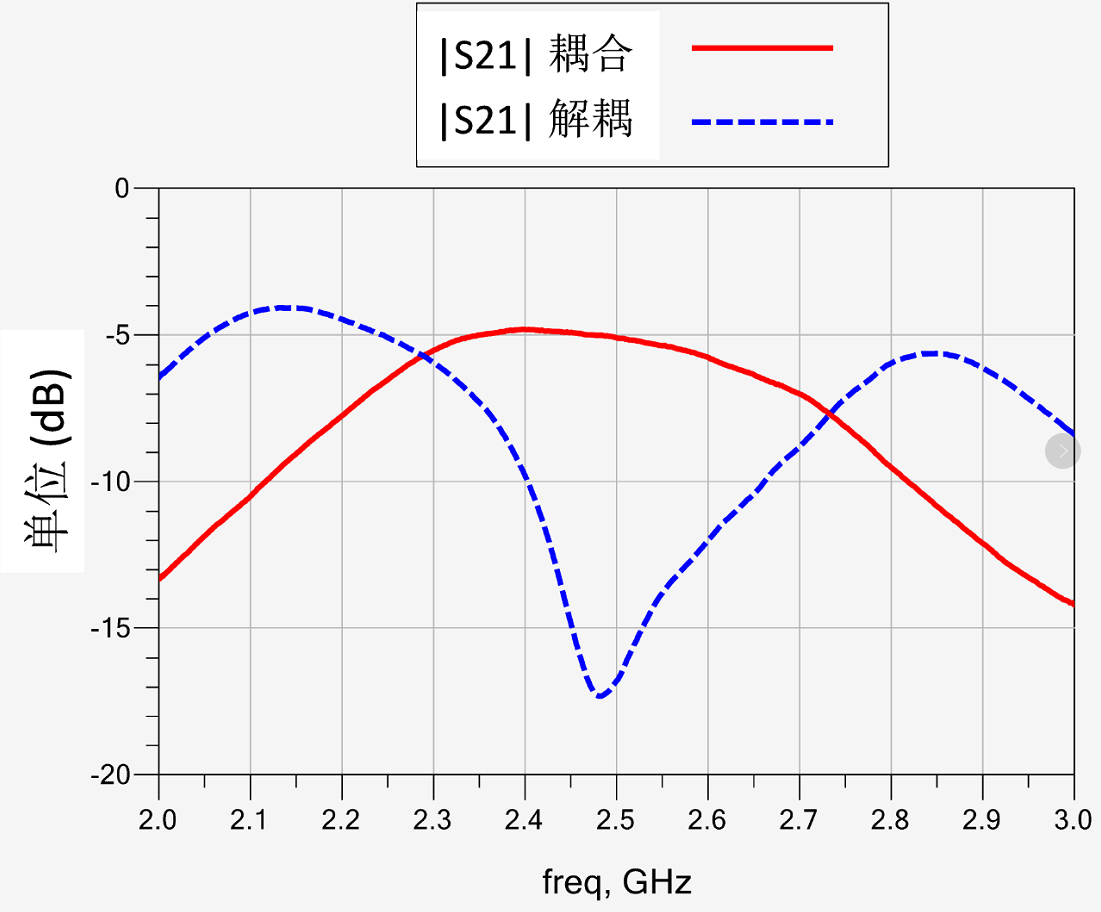
解耦前后,图3中两组天线S参数的比较请参见图4。由图4可以看出,原来耦合天线虽然匹配满足要求,但是隔离度只有5至6dB,这说明有25%以上的能量没有有效辐射,而是被另一天线负载吸收。在合理优化设计去耦合芯片AIR之后,匹配状态没有明显恶化的情况下,隔离度提高到10至15dB,此时耦合的能量已经小于10%。可以看到AIR对提高天线隔离度的明显作用。

图 3 (a)耦合双天线 (b) 解耦双天线
(a)
(b)
(c)
图 4 解耦前后两天线的(a)S11,(b)S22和(c)S21的幅度响应
参考文献
1 M. A.Jensen and J. W.Wallace, “A review of antennas and propagation for MIMOwireless communications,” IEEE Trans. Antennas Propag., vol., 52, no. 11, pp.2810–2824, Nov. 2004
2 J. B.Andersen and H. H. Rasmussen, “Decoupling and descattering networks forantennas,” IEEE Trans. Antennas Propag. vol., 24, no. AP-6, pp. 841-846, Nov.1976.
3 L. K.Yeung and Y. E. Wang, “Mode-based beamforming arrays for miniaturizedplatforms,” IEEE Trans. Microw. Theory Tech., vol. 57, no. 1, pp. 45-52, Jan.2009.
4 B. K.Lau and J. B. Andersen, “Simple and efficient decoupling of compactarrays with parasitic scatterers,” IEEETrans. Antennas Propag., vol. 60, no. 2, pp. 464‐472, Feb.2012.
5 Luyu Zhao; Ke-Li Wu “A DecouplingTechnique for Four-Element Symmetric Arrays With Reactively Loaded DummyElements”, IEEE Trans. Antennas Propag., vol. 62, No. 8, pp. 4416 – 4421, Aug.2014.
6 L. Zhao, L. K. Yeung, and K.-L. Wu,”A novel second-order decoupling network for two-element compact antennaarrays,” Proc. Asia-Pacific Microwave Conf., pp. 1172 – 1174, Dec. 2012.
7 L. Zhao and K.-L. Wu, “A broadbandcoupled resonator decoupling network for a three-element compact array,”Proc. IEEE MTT-S Int. Microw. Sym., Jun. 2013.
8 L. Zhao, L. K. Yeung, and K.-L. Wu, “A coupled resonator decoupling network for two-element compact antenna arraysin mobile terminals,” IEEE Trans. Antennas Propag., vol. 62, no. 5,pp.2767-2776, May 2014.
